이산수학 - 10. 부울대수 + 고급 계수 기법

1. 부울대수

2. 부울대수의 표현

3. 정규식의 간략화

4. 점화관계

5. 분할정복 알고리

6. 포함-배제

 

 

 

1. 부울대수

부울대수: 0과1을 입력값으로 갖는 논리계산을 형식화한 것 

논리회로를 설계할때 사용하며 간단한 논리회로를 설계하기 위함이다.

부울변수: 0또는 1의 값을 받는 변수

부울함수: n개의 부울 변수와 부울 연산자로 구성되는 식: n차 부울함수

부울보수: 2진 변수의 값을 반전시키는 단항 연산자

부울합: 2진 변수의 값을 더하는 이항 연산자 (0+0=0, 0+1=1+0=1+1=1)

부울곱: 2진 변수의 값을 곱하는 이항 연산자 (0*0=0*1=1*0=0, 1*1=1)

부울곱과 부울합의 기호와 산술연산의 곱셈, 덧셈 기호는 생긴 것이 같지만 의미는 다르다.

 

 

 

2. 부울함수의 표현

최소항(Minterm): n 차 부울함수를 구성하는 논리곱 항들 중 n개의 리터럴(n차 부울함수를 구성하는 부울변수나 그 보수) 곱으로 구성된 항

• f(x,y) = x'+y: 첫번째 항을 구성하는 리터럴은 x의 보수(x')고, 두 번째 항을 구성하는 리터럴은 y. (1)의 2차 부울함수를 구성하는 리터럴은 x'와 y 두개이다.
• f(w,x,y,z) = w'x'y'z' + w + xy' + wyz' + xz': 리터럴은 w', x', y', z', w, x, y 이다.

정규식(DNF: Disjunctive Normal Form): 최소항들의 부울합으로 표현된 부울함수

• f(x,y) = x+xy': 첫번째 항이 2개의 리터럴이 아니므로 정규식 X
• f(x,y,z) = x'z+xy'z'+z: 첫번째, 세번째 항이 3개의 리터럴이 아니므로 정규식 X
• f(w,x,y,z) = w'x'yz+w'x'y'z+wxyz: 모든 항이 4개의 리터럴로 되어있으므로 정규식 O

정규식이 아닌 부울함수를 정규식으로 표현하는 방법

1. 각 항에 포함되지 않은 부울변수를 파악한다
2. 각 항에 포함되지 않은 부울변수에 대해 논리곱에 대한 항등법칙 x*1=x와 논리함에 대한 보수법칙 x+x'=1을 적용해 각항에 없는 부울변수를 추가한다.
3. 분배법칙 등을 이용해 식을 풀고, 중복되는 항은 멱등법칙에 의해 제거한다

 

 

 

3. 정규식의 간략화

부울대수법칙을 이용한 간략화: 정규식을 간략화 하는 방법과 같은 방식

 

예제) 다음 정규식을 간략화하라

f(x,y) = xy'+x'y+x'y' = xy'+x'(y+y') = xy' + x' = (x+x')(y'+x') = x'+y'

 

카르노 맵을 이용한 간략화: 2변수이상 6변수 이하의 부울함수에 사용

카르노 맵: 부울함수에서 사용되는 변수에 대한 2진수 조합의 개수만큼 2차원 평면상에 셀을 배열하고, 부울함수에 있는 변수들의 조합을 표시하여 만든다.

2변수, 3변수 카르노 맵 카르노맵의 변수 순서는 2진수를 사용하여 나타낼 때 정수의 크기순이다.

카르노맵을 이용하여 간략화 하는 방법

1. n차 부울함수에 대응하는 n변수 카르노맵을 선택
2. 부울함수에 있는 항들 각각에 대응하는 카르노맵 셀에 1을 표시
3. 인접하는 1들을 2의 제곱수 (보통 8,4,2 순으로 묶음) 로 묶는다.
4. 묶음에 있는 공통변수들을 찾아 논리합으로 묶는다.

 

예제) f(w,x,y,z) = wxy'z' + wxyz' + wx'yz + wx'y'z' + wx'yz' + w'x'yz + w'x'y'z + w'x'yz + w'xyz + w'xy'z' + w'xyz'를 간략화 하라

 

1. 4변수 카르노맵을 사용한다.

2. 부울함수에 포함된 항들을 카르노맵에 1로 표기한다

3. 인접한 항들을 찾기 위해 16(2^4), 8, 4, 2개의 1이 인접하는지 확인한다. 인접한 1끼리 묶는다.

4. 각 묶음에 공통으로 있는 변수를 찾아 논리합으로 묶는다.

묶음 a의 공통변수: z'

묶음 b의 공통변수: w'y

묶음 c의 공통변수: x'y

f(w,x,y,z) = w'y + x'y + z

 

 

 

 

4. 점화관계

점화관계(recurrence relation, = 재귀식): 하나 이상의 초기 항들과 그들로부터 그다음 항들을 결정짓는 규칙을 통해 반복적인 방법으로도 정의하는 것. 이러한 점화관계를 만족시키는 수열을 점화관계의 해라고 한다.

 

• 피보나치 수: (fn = fn-1 + fn-2)
• 하노이 탑: n개의 원반을 갖는 하노이 탑 문제를 풀기위해 요구되는 이동의 수 Hn은 (Hn = 2Hn-1+1, H1=1)
  • Hn = 2Hn-1 +1 = 2(2Hn-2 + 1) + 1 = 2^2Hn-2 + 2+1.... = 2^n-1 

수학적 귀납법을 이용한 재귀식 구하기 (경북 20 기출) 

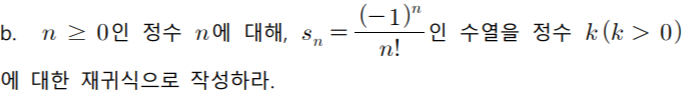
Sk = Sk-1 * S1임을 이용하여 풀이한다.

 

 

 

 

+) 기타

 

분할정복(Divide and conquer): 더 작은 크기를 갖는 문제들로 나누고 더 작은 문제의 해를 사용하여 원래 문제의 해를 구함으로써 정복한다 (이진탐색, 병합정렬)

 

포함-배제: