이산수학 - 4. 행렬

1. 행렬의 개념

2. 행렬의 연산

3. 행렬의 종류

4. 행렬식

5. 역행렬

6. 연립 1차 방정식

 

 

1. 행렬

m,n이 양의 정수이고 n행, m열로 나열된 실수의 2차원 배열(Matrix) 

가로줄이 행, 세로줄이 열이다.

 

2. 행렬의 연산

행렬의 덧셈과 뺄셈: 두 행렬 A, B 의 같은 자리에 있는 원소끼리 더하거나 뺌

 

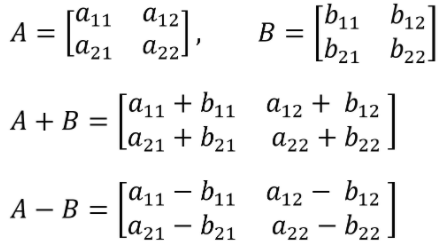
행렬의 스칼라 곱: 행렬 A에 실수 k를 곱하는 연산 kA

행렬의곱셈: m*n 행렬 A와 r*s 행렬 B가 있고 n=r 일때, m*s 행렬 AB의 각 원소는 A*B로 구함 

• 행렬A의 열 크기(가로줄)와 행렬 B의 행 크기(세로줄)의 크기가 같아야 한다.
• m*n, r*s 행렬을 곱할때, 결과 행렬은 m*s이다. Sms 자리에 곱한 값이 들어간다.

 

 

3. 행렬의 종류

영행렬 (Zero Matrix, O): 모든원소가 0인 행렬

n차 정사각행렬(n-Square Matrix): n*m인 행렬 A가 있을때 m=n인 행렬

대각행렬(Diagonal Matrix): 정사각행렬에서 대각원소 a11, a22, a33, ... , anm이외의 모든 원소가 0인 행렬

단위행렬(Unit(Identity) Matrix, I): 대각행렬에서 모든 대각원소가 모드 1인 행렬

전치행렬(Transpose Matrix, At): m*n 행렬A가 있을때 행과 열을 바꾼 n*m 행렬

대칭행렬(Symmetric Matrix): At = A인 행렬 (대각원소를 기준으로 n,m을 바꿔도 행렬의 원소가 동일한 행렬)

부울행렬(Boolean Matrix): 행렬의 모든 원소가 0,1로만 구성된 행렬

• 부울 행렬에 대해서 합(A∨B), 곱(A∧B), 부울곱(A⊙B) 연산이 가능하다.

 

4. 행렬식

행렬식(Determinant) (det(A)): n차 정사각행렬에 대응하는 수를 구하는 식

• 작은 규모의 연립방정식의 해를 구하거나 
• 가역행렬이기 위한 필요충분조건 det(A) != 0
• 연립방정식 해의 존재성을 살피려고 할때 사용

출처: http://www.ktword.co.kr/abbr_view.php?m_temp1=4650

출처:http://www.ktword.co.kr/abbr_view.php?m_temp1=4650

소행렬(Minor Matrix): n차 정사각행렬에서 r번째 행과 s번째 열을 제거해서 얻은 (n-1) * (n-1) 행렬

• det(Mrs): r행과 s열을 제외한 행렬에서 행렬식을 구한 것.

여인수(Cofactor): n차 정사각행렬 A에서 소행렬에 대한 행렬식을 이용하여 계산한 값, 행렬식을 구하는데 이용하는 표기식

여인수 행렬(Cofactor Matrix): n차 정사각행렬 A에서 원소 aij에 관련된 수와 그 수들에 대한 행렬, 행렬 A와 크기는 같고 각 성분이 여인수로 이루어진 행렬

 

예제) 다음 행렬의 각 원소에 대한 여인수를 구하여 여인수 행렬을 구하라

 

 

 

여인수를 이용한 행렬식: 주어진 행렬의 행이나 열 중 하나를 선택하여 해당하는 원소의 여인수와 곱한 후, 그 결과값을 더하여 행렬식을 구한다. 이때, 행이나 열은 연산을 가장 간단하게 유도할 수 있는 것으로 선택한다. (어떤 행이나 열을 선택해도 답은 똑같다.)

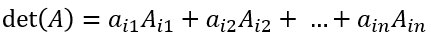
i행을 선택한 경우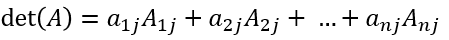

 

j열을 선택한 경우

 

 

 

5. 역행렬

역행렬(Inverse Matrix): 정사각행렬 A에 대해 AB = BA = I(단위행렬) 를 만족하는 행렬 B

• 아래와 같은 방법은 차수가 높아질수록 변수가 많아져 행렬식과 여인수, 전치행렬을 이용해 역행렬을 구한다.

 

행렬식을 이용한 역행렬:

 

 

 

 

수반행렬: 여인수행렬에 대한 전치행렬(행과 열을 바꾼 행렬)

가역행렬: 역행렬이 존재하는 행렬(행렬식의 값이 0이면 역행렬식의 분모가 0이 되므로 역행렬이 존재하지 않는다.)

특이행렬: 역행렬이 존재하지 않는 행렬

 

 

 

6. 연립1차 방정식

연립1차 방정식은 계수와 미지수 상수로 구성되어있기 때문에 다음과 같이 표현할 수 있다.

 

가우스 소거법: 계수행렬의 대각원소들을 모두 1로 만들고 대각원소를 기준으로 아래쪽 원소들은 모두 0으로 만든 후 위쪽 원소들은 계수들로 남겨놓은 형태의 첨가행렬(행렬로 나타냈다 뿐이지 기존의 연립방정식 풀이와 유사하다)

1. 한 행에 0이 아닌 상수를 곱한다.
2. 상수배한 행과 다른 행을 더해 원소를 0으로 만든다.
3. 필요에 따라 행을 교환할 수도 있다.

 

가우스 조르단 소거법: 가우스 행렬의 계수행렬 부분을 단위행렬(모든 원소가 1)로 만들어 해를 얻는다. (나머지 영역은 0으로 만들어야함))

 

 

 

 

편입 면접 기출

부산대 (2010): 행렬의 대칭, 비대칭 구분

대각원소를 기준으로 행과 열을 서로 바꿔도 본래 행렬과 동일한 행렬.